Chapter 3 parallel and perpendicular lines answers – Chapter 3: Parallel and Perpendicular Lines—Unveiling Their Interplay, delves into the captivating world of geometry, where lines dance in harmonious patterns. This chapter unveils the intricacies of parallel and perpendicular lines, exploring their definitions, properties, and applications.
Parallel lines, like celestial bodies in orbit, maintain a constant distance from each other, never crossing paths. Perpendicular lines, on the other hand, intersect at right angles, forming a crisp 90-degree embrace.
Parallel and Perpendicular Lines Basics
In geometry, lines that share a constant distance from each other are known as parallel lines. Perpendicular lines, on the other hand, intersect at a right angle (90 degrees).
Examples of parallel lines include the edges of a rectangular table, the sides of a square, or the rails of a railway track. Perpendicular lines can be seen in the corners of a room, the intersection of a cross, or the meeting point of a wall and a ceiling.
Properties of Parallel and Perpendicular Lines
- Parallel lines never intersect.
- Perpendicular lines intersect at right angles.
- The distance between two parallel lines remains constant.
- Perpendicular lines form two congruent adjacent angles (45 degrees each).
Identifying Parallel and Perpendicular Lines
Identifying Parallel Lines
Parallel lines can be identified by using the following methods:
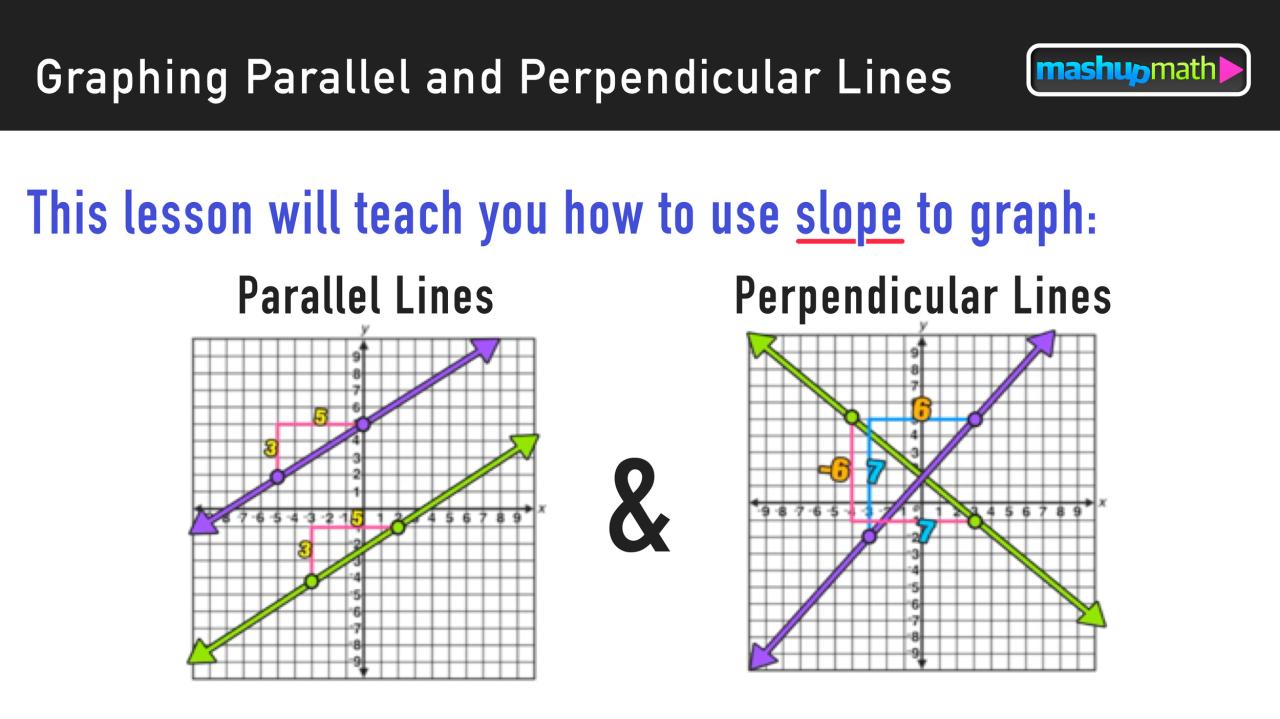
- Slope:Parallel lines have the same slope.
- Intercepts:Parallel lines have different intercepts.
- Angle Measurements:Lines that form congruent alternate interior angles are parallel.
Identifying Perpendicular Lines
Perpendicular lines can be identified by using the following techniques:
- Slope:Perpendicular lines have slopes that are negative reciprocals of each other.
- Angle Measurements:Lines that form a right angle (90 degrees) are perpendicular.
Angle Relationships in Parallel and Perpendicular Lines: Chapter 3 Parallel And Perpendicular Lines Answers
Relationship Between Parallel Lines and Angles
Parallel lines create specific angle relationships:
- Alternate Interior Angles:When a transversal intersects two parallel lines, the alternate interior angles are congruent.
- Alternate Exterior Angles:When a transversal intersects two parallel lines, the alternate exterior angles are congruent.
- Corresponding Angles:When a transversal intersects two parallel lines, the corresponding angles are congruent.
Perpendicular Bisectors
A perpendicular bisector is a line that passes through the midpoint of a line segment and is perpendicular to it.
Properties of Angles Formed by Parallel and Perpendicular Lines, Chapter 3 parallel and perpendicular lines answers
- Angles formed by parallel lines and a transversal are supplementary (add up to 180 degrees).
- Angles formed by perpendicular lines are complementary (add up to 90 degrees).
Q&A
What is the difference between parallel and perpendicular lines?
Parallel lines never intersect, while perpendicular lines intersect at right angles.
How can I identify parallel lines?
Parallel lines have the same slope and do not intersect.
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.